算数の分数の学習も大詰めです。子どもたちに,「正しい長さはどれでしょう」と投げかけます。提示された長さに合う図を探します。
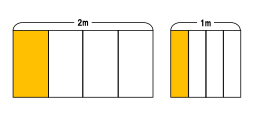
3問目の問題で,「1/4m」の長さを尋ね,右図を提示
します。正しいと思う図を,左手・右手・両手で指させることにしました。この問題では,子どもの意見は分裂しました。
右図は「1mを4等分した内の1つ分だから1/4m」と全員が納得しました。一方,意見が分かれたのが左図です。多くの子どもが,左も1/4mと考えました。その根拠を,子どもたちに考えさせます。
「2mを4等分した内の1つ分だから1/4m」
「1mの1/4は25㎝。でも,2mの1/4は50㎝だから,左は違う」
「もし8mのテープを1/4にしたら,それは2m。1/4mは1mより短いはずなのに,1mより長いから1/4mではない」
1/4mの長さを㎝に置き換えると25㎝です。この視点からの説明ですが,1/4mだと考える子どもたちは納得しません。「だって,2mの1/4。だから1/4m」と主張します。分割分数と量分数を混同しているのです。3年生にはよく見られる光景です。
すると,今度は次の声が聞こえてきます。
「1mは左から順に1/4m,2/4m,3/4m,4/4mとなって1mになる。でも,左の図が1/4mだとしたら,左から1/4m,2/4mとなるけど,そこは1mの場所。2/4mが1mはおかしい」
「8mの1/4は2mでしょ。1mを超えている。左の図が1/4mならこれも1/4mになるのは変だ」
左の図が1/4mだとしたらと仮定した考えると,テープの色の部分が増えていくと不都合が生まれてくるという説明です。素晴らしい視点からの説明です。しかし,これらの説明で「えー,分かんなくなってきた」と混迷に陥る子どもも生まれてきました。残念ながらここで時間切れ。子どもの話し合いはどうなるのでしょうか・・・。