３年生の子どもたちに，次の問題を提示します。
「紙テープがあります。赤は青の２倍の長さです。黒は赤の３倍の長さです。黒は赤の何倍ですか」
問題に出会った子どもからは，「？」「頭の中がごちゃごちゃしてきた」などの声が聞こえてきました。問題場面が複雑で，うまくイメージができないのです。
そこで，頭の中のごちゃごちゃを解消するにはどうしたらよいのかを考えます。子どもたちは「図にすると分かりやすい」と考えました。
すると今度は子どもから，「５倍だね」「えっ？６倍でしょ」と，青と黒のテープが何倍の関係に当たるのかを考える声が聞こえてきます。
そこで，「５倍と考えた友だちの気持ちは分かるかな？」と，５倍の気持ちの読解を行います。
「青から赤が２倍。赤から黒が３倍。だから，これを合わせたら５倍になる」
この説明に子どもたちも納得です。しかし，「でも！」とこの論理を否定する声が聞こえてきます。一方，「５倍でしょ」という声も聞こえてきます。
いったい５倍なのか，６倍のなのか？ 子どもの中から，「だったら長さを入れたらいい」と声が聞こえてきます。ここまでは具体的な長さがない状態で，青と黒の関係を考えていました。しかし，これでは５倍か６倍かがはっきりとしません。そこで，具体的な数値を入れれば分かるというアイディアです。
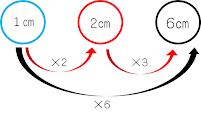
「もし青が１㎝なら，赤は２倍の２㎝。そうすると，黒は２㎝の３倍だから６㎝」
具体的な数値で考えることで，子どもたちも青を黒の関係が６倍になることを全員が納得をしました。
抽象的な場面に意図的に出会わせることで，具体的な数値を使って考える良さを子どもたちは実感していくことができました。
その後，テープ図を作図しても６倍の関係が見えることも分かりました。
