田中博史先生と盛山隆雄先生の共著「子どものためにきょうしができること」の本に,田中先生が4年生に実施した面積の授業が掲載されていました。その教材をアレンジして,1年生に授業をしてみました。
次のように投げかけます。
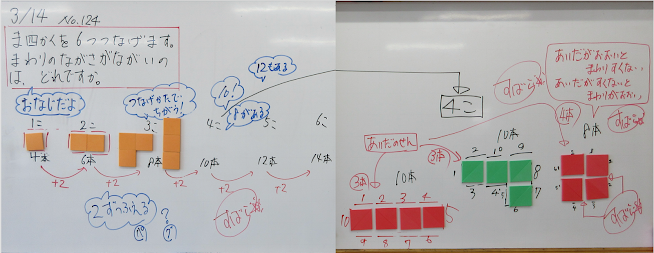
「真四角を6つつなげます。周りの長さが長いのは,どれかな?」
田中先生は正方形4つをつなげていましたが,私は6つの場合で試そうと考えました。ところが・・・。
問題文を提示すると同時に聞こえきたのが「同じだよ」という呟きです。そこで,この意味を読解するところからスタートします。
「真四角2個なら,周りは6本でしょ」
問題文は真四角6個ですが,例示として真四角2個の考えが生まれてきました。そこで,2個の場合の周りの場所を確認することにしました。周りの意味の共通認識が必要だからです。
2個の周りを確認すると,今度は次の声が聞こえてきました。
「1個なら周りは4本だね」
「あ!2個ずつ増える」
「1個は4本,2個は6本で2本増えてる。だから,真四角3個も2本増える」
「2ずつ増えるから,真四角3個は8本,4個は10本,5個は12本,6個は14本になる」
正方形2個,1個と例示が生まれてきたことで,子どもたちはそこに関数的な関係性を見出していきました。すると子どもたちの関心は,正方形が3個つながった形の周りの長さに向かいます。私が問題文で提示した正方形6個の場面は,この瞬間どこかに行ってしまいました・・・。
3個の場合を実験する前に聞こえてきたのが,「つなげ方で違うんじゃない」という声です。正方形1個・2個でできる形は1通りです。しかし,3個は1通りではありません。このイメージが子どもにもあるのでしょう。そこから生まれてきた声です。この声の誕生で,子どもたちも不安になります。
そこで,3個を実験します。ところが,つなげ方を変えても,周りの長さは8本でした。
「だったら,4個は10本だ」
この声が当然のように生まれてきます。今度は子どもは自信満々です。そこで,早速実験開始です。ところが,しばらくすると聞こえてきたのが,「あれ,8個ある」「10個できた」「12個もある」の声でした。そこで,できた図形を板書します。
完成したのは10本と8本の2種類です。子どもからは「なんで8本?」と疑問の声が聞こえてきます。10本は予想通りですが,8本は予想外の結果です。予想とのズレとの出合いです。
するとここで,「秘密が分かった」の声があがります。
「8本は間が4本ある。10本は間が3本しかない」
「間が多いと周りが少なくて,間が少ないと周りが多くなるんだよ」
正方形2個が接することでできるのが図形に内包された部分の線です。その数と外部の辺の数に関係性を見出したのです。この声に「本当だ!」「びっくり」と声があがります。しかし,この見方は一般化できるのでしょうか。ほとんどの子どもたちは,この関係性の発見に自信満々です。しかし,授業はここで時間切れでした。
私の当初に用意した問題場面に入ることはできませんでしたが,私がねらっていた見方・考え方は想定以上に引き出すことができました。賢いこどもたちです!