2年生の大きな数のひきざんの一コマです。
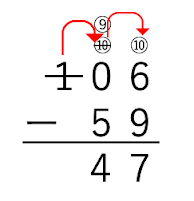
「難しい度アップアップ問題」と命名されたひかれる数の十の位が0のひきざんに取り組みました。右のような「106-59」の計算をノートに行います。
答えが47と求められたあとのことです。子どもから次の声があがってきます。
「繰り下がりは2回だったね」
「えっ? 1回でしょ」
「違うよ。2回だよ」
大人が考えると,繰り下がりは2回に見えます。ところが半数ほどの子どもたちは,繰り下がりは1回だと考えました。子どもたちの論理を予想できるでしょうか。
「繰り下がりは1回。だって,百の位から十の位と一の位に10をプレゼントしたんだから,1回」
「そうじゃないよ。借りているのは10と10の2個だから2回」
「そうだよ。百の位から十の位に100をプレゼントしたでしょ。これは10が10個。次に,その中の1個の10を一の位にプレゼントしたでしょ。百の位から十の位で1回,十の位から一の位で1回だから2回だよ」
「やっぱり1回だよ。だって,借りてきた元は百の位でしょ。元は百の位の1個なんだから1回だよ」
これまで子どもたちが学習してきた繰り下がり2回の計算は,
右のようなタイプです。これは一の位が引けないので十の位から10を借ります。十の位も引けないので百の位からも10を借ります。借りる元が十の位と百の位と2カ所あります。
ところが今回の問題は,元々の借りる先は百の位の1カ所です。そこから十の位に一旦繰り下げ,そこからさらに一の位に又貸しをする形になります。これが繰り下がり1回と考える子どもたちの論理です。借金で例えると,借りた先は百の位だけで,十の位は単に橋渡しをしただけの存在ということになります。
10を借りてきた元々の場所の数で考えたら1カ所,これが1回と考える論理の根拠です。一方,繰り下がりの手続きの回数で見たら,2回の手続きを行っています。これが2回と考える論理の根拠です。
両者の言葉の違いから,論理の違いが明確になった授業となりました。